Originaler Artikel vom November 2020 wurde auf der Akademie Tutorium Berlin Seite veröffentlicht
Hallo zusammen! Mich hat in den letzten Tagen der MiniMax Algorithmus interessiert.
Kurz gesagt ist es ein Algorithmus, der in einem Spiel mit mehr als einem Spieler (normalerweise zwei) die optimale Strategie zum Gewinnen findet. Hier eine sehr gute Erklärung, ist allerdings auf Englisch:
Damit der Algorithmus in ein Spiel passt, ist es Voraussetzung, dass es ein auf Zügen basierendes Spiel ist, in dem man jeder Position des Spiels einen Wert zuteilen kann:
Im Fall von TikTakToe wären das zB.:
Beide Spieler haben keine Dreier-Reihe voll = kein Wert (weil das der normale Zustand des Spiels ist)
Ein Spieler hat eine dreier Reihe = ‚1‘ für einen Spieler und ‚-1‘ für den anderen
Das Spielbrett ist voll (Unentschieden) = 0
Es gibt andere Möglichkeiten, den Zustand des Bretts zu bewerten, aber das ist die einfachste für den Algorithmus.
MiniMax sucht dann durch jeden möglichen Zug, den der Spieler machen kann, nach jedem Möglichen Zug den der Gegenspieler nach diesem möglichen Zug machen kann, nach jedem möglichen Zug des Spielers nach jedem möglichen Zug des Gegenspielers nach jedem möglichen Zug des Spielers usw…
Wichtig ist, dass MiniMax immer davon ausgeht, dass der Gegenspieler für ihn optimale Züge macht. Wenn er es dann nicht machen sollte, ist es noch besser für den Spieler…
Diese Suche endet, sobald ein möglicher Zug eine Endposition erreicht. In unserem Fall also eine Position mit dem Wert von 1, -1 oder 0.
Der Wert wird dann bis zum Anfang dieser Kette hochgereicht und diesem möglichen Zug, der zur Endposition geführt hat, zugeschrieben. Der Spieler bzw. die „Künstliche Intelligenz“ wählt jetzt einfach einen Zug aus, der auf dem Pfad zum „Sieg“ oder dem bestmöglichen Ergebnis liegt.
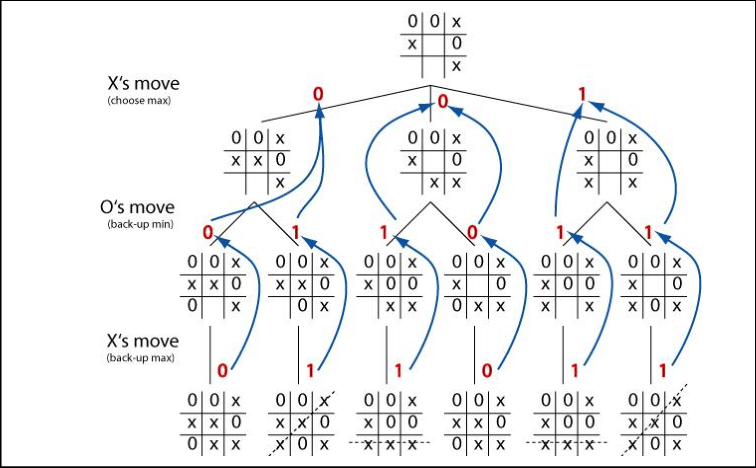
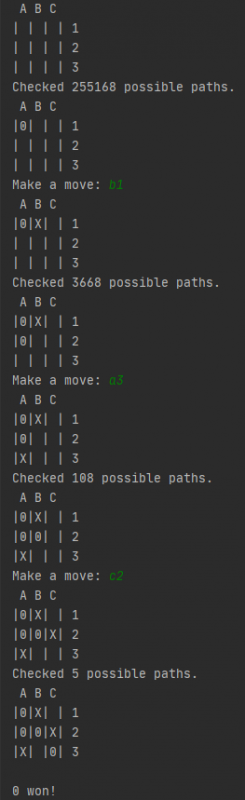
Am Start eines normalen 3×3 Feldes läuft MiniMax durch 255.168 mögliche Pfade, die zu einer Endposition führen. Die Anzahl an möglichen Pfaden verringert sich schnell nach jedem gemachten Zug.
Gegenspieler ohne MiniMax = X
Die KI macht in diesem Fall den ersten Zug
Zug 1: 9x8x7x6x5x4x3x2x1x0,7 = 254.016* mögliche Pfade
Zug 2: 8x7x6x5x4x3x2x1x0,7 = 28.224*
Zug 3: 7x6x5x4x3x2x1x0,7 = 4.032* usw.
* Diese Zahlen sind wie man sieht grob gerechnet und ungenau. Da es Endpositionen vor dem Füllen des gesamten Bretts gibt, fallen ungefähr 30% der Pfade weg.
(255.168 : 326.880 ≈ 0,7) ist für ein 3×3 Feld berechnet. Die Zahl ist wahrscheinlich anders in anderen Szenarien.
Das bedeutet allerdings auch, dass die Anzahl mit nur ein wenig mehr Feldern explodiert. Ein 4×4 Brett (also 16 mögliche Startpositionen) hat 14.645.952.921.600 mögliche Pfade, die zu einer Endposition führen. Ein 3×3 Feld hat also 0,0000017% der möglichen Pfade eines 4×4 Brettes.
Möglichkeiten zur Optimierung
Für den ersten Zug in einem 3×3 Feld braucht MiniMax auf meinem Computer ca. 30 Sekunden.
In einem 4×4 Feld würde es 20 Tage dauern. Ein wenig zu lange 😉
Jetzt stellt sich also die Frage, wie man den Algorithmus optimieren kann…
Alpha Beta Pruning
Alpha Beta Pruning ist eine Möglichkeit, um die zu durchsuchenden Pfade zu reduzieren, in dem der Algorithmus aufhört einen Pfad zu verfolgen, wenn es eine bessere Möglichkeit gibt und durch optimales Spielen keiner der Spieler diesen Pfad gehen würde. Alpha Beta Pruning ist sehr gut im Video oben erklärt.
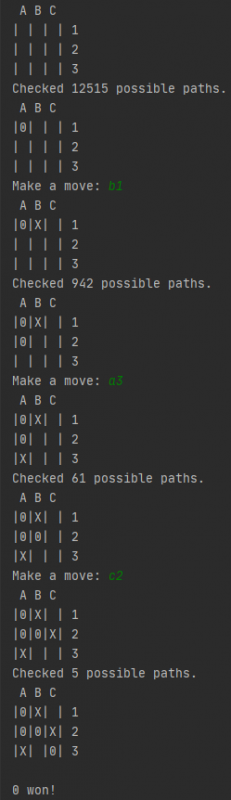
Komplexere Bewertung von Spielpositionen
Eine andere Möglichkeit, wenn man nicht alle Pfade bis zum Ende durchsuchen will ist, dass man die Anzahl an Zügen, die MiniMax in die Zukunft schaut, begrenzt und die Spielposition besser/komplexer bewertet, also nicht nur Situationen, die entweder unentschieden sind oder in denen ein Spieler gewonnen hat, bekommen einen Wert, sondern z.B. auch:
Beide Spieler haben keine Dreier-Reihe voll = kein Wert (weil das der normale Zustand des Spiels ist)
Endpositionen:
Ein Spieler hat eine Dreier-Reihe = ‚∞‘ für einen Spieler und ‚-∞‚ für den anderen
Das Spielbrett ist voll (Unentschieden) = 0
„Checkpoints“:
Ein Spieler vereitelt eine Dreier-Reihe = 0 (das hätte in der vorherigen Bewertung keinen Wert erhalten)
Ein Spieler setzt seine Figur in ein Feld bzw. eine Reihe, in der genügend Platz für eine volle Dreier-Reihe ist = ein kleiner Wert
Ein Spieler hat gebaut bzw. baut eine Zwickmühle = ein Wert, der den Fortschritt des Zwickmühlen-Baus spiegelt
etc.
Extra Bewertungen oder „Checkpoints“, wie ich sie hier genannt habe, machen nicht viel Sinn in einem 3×3 Feld, aber für größere Felder mit unterschiedlichen Gewinnlängen sieht das anders aus.
„Checkpoints“ setzen meistens darauf, dass der Gegenspieler einen Fehler macht. Weil MiniMax immer davon ausgeht, dass der Gegenspieler optimale Züge macht, kommt man sonst in Situationen, in denen die KI nicht einmal versucht, das Gewinnen des Gegners zu verhindern, weil sie keinen Unterschied zwischen dem Versuch, das Gewinnen des Gegners zu verhindern und nichts tun sieht… ziemlich hoffnungslos also ^^
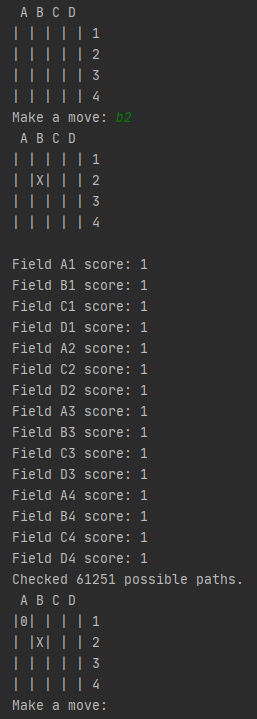
MiniMax schaut 6 Züge in die Zukunft.
Die KI ist der minimierende Spieler (der negative Werte erreichen will). Die 1 bedeutet für die KI also, dass sie mit diesem Zug verlieren würde…
Für die KI sind alle Züge gleich, weil der optimale Gegenspieler innerhalb von 6 Zügen mit einer Zwickmühle gewinnen würde, ohne dass die KI etwas dagegen tun könnte.
Erkundete Pfade speichern
Dass MiniMax in einem 3×3 Feld durch 255.168 mögliche Pfade sucht, bedeutet nicht, dass ein 3×3 Feld so viele mögliche Konfigurationen hat. Der Algorithmus durchsucht die selben Pfade einfach immer wieder, was natürlich vom Standpunkt der Effizienz ziemlich bescheuert ist. Eine Optimierungsmöglichkeit ist also, erkundete Pfade zu speichern. Wenn man dem selben Pfad nochmal über den Weg läuft, schaut man einfach im Speicher nach dem gegebenen Wert und muss nicht alles nochmal durchrechnen…
Das waren alle Optimierungsmöglichkeiten, die mir im Moment zum Algorithmus einfallen. Falls dir eine andere einfällt, würde ich mich freuen sie zu hören!
Minimax Python Code:
def minimax(position, depth, alpha, beta, maximizingPlayer, grid_size, winning_length):
depth_count = 0
result = check_board_status(position, grid_size, winning_length)
if depth == 0:
return 0, depth_count + 1
elif result is not None:
return result, depth_count + 1
if maximizingPlayer:
maxEval = -float("inf") # maxEval is set to negative Infinity
brk = False
for y in range(len(position)):
if brk:
break
for x in range(len(position)):
if position[y][x] == " ":
position[y][x] = "X"
temp_eval, recovered_depth = minimax(position, depth - 1, alpha, beta, False, grid_size, winning_length)
position[y][x] = " "
maxEval = max(maxEval, temp_eval)
depth_count += recovered_depth
# Alpha Beta Pruning
alpha = max(alpha, temp_eval)
if beta <= alpha:
brk = True
break
return maxEval, depth_count
else:
minEval = float("inf") # minEval is set to Infinity
brk = False
for y in range(len(position)):
if brk:
break
for x in range(len(position)):
if position[y][x] == " ":
position[y][x] = "0"
temp_eval, recovered_depth = minimax(position, depth - 1, alpha, beta, True, grid_size, winning_length)
position[y][x] = " "
minEval = min(minEval, temp_eval)
depth_count += recovered_depth
# Alpha Beta Pruning
beta = min(beta, temp_eval)
if beta <= alpha:
brk = True
break
return minEval, depth_count
Link zum kompletten Python Code, falls du damit rumspielen möchtest 😀
Ich hoffe dieser Artikel war interessant! Ich freue mich über jegliche Art von Feedback bzw. Änderungen im Code!
Quellen:
Bild: Minimax für TikTakToe dargestellt
aus: A Comparative Study of Game Tree Searching Methods
von: den Autoren des besagten Artikels
unter: Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International
